DataStructure

Francessca Lv1
  2024-12-29 11:44:03 2024-12-29 11:44:03 Created   2024-12-29 14:26:32 2024-12-29 14:26:32 Updated  

1. Class in C++

1.1 Data Structure

Data Structure refers to a collection of data elements with interrelationships and structures, including data logical structure,data storage structure,and data operation.

1.2 Class in C++

  • A class consists of variables, called fields,together with Functions,called method, that act on fields.
  • Method Interface: the explicit information a user will need in order to invoke the methods.
  • Object: a variable whose type is a class, an instance of its class.
  • User’s view of a class: method interface(= precondition + postcondition | method heading)
  • Developer’s view of a class: fields and method definitions
  • Inheritance: the ability to define a new class(subclass) that includes all the fields and some or all of the methods of an existing class(superclass). The subclass may declare new fields and methods, and may override existing methods.

1.3 Principle of data abstraction

A user’s code should not access the implementation details of the class used.

1.4 The open-closed principle

Every class should be

  • Open: Extendible through inheritance
  • Closed: Stable for existing applications

1.5 Subclass substitution rule

Whenever a superclass object is called for in an expression, a subclass object may be substituted.

2. Container Classes

2.1 Dynamic variable

  • A dynamic variable is one that is created and destroyed by the programmer during execution.(this can save a lot of space in memory).
  • Dynamic variables are stored in the heap,a large area of memory
  • Dynamic variables are never accessed directly. They are accessed through pointer variables.
    • A pointer variables contains the address of a variable
    • A pointer type is a type followed by an asterisk: String* sPtr;
  • To create a dynamic variables, the new operator is used: sPtr = new string;
  • To access the dynamic variable, we dereference the pointer variables by the dereference operator,’*****’,is place in front of the pointer variables: *sPtr
  • The dereference-and-select operator is ->,sPtr->length()<=6 is equivalent to (*sPtr).length < = 6
  • The destroy a dynamic variables the delete operator is used: Delete sPtr;

2.2 Arrays

  • string* words; Here, words can be a pointer to either a single string or to an array of strings.
  • Pointer to an array of strings: words = new string[7];
  • The index operator [], is used to reference the individual items: words[1] is equivalent to *(words+1) (Universal array-pointer law)
  • Random-access: any item in an array can be accessed or modified immediately given the index of the item
  • To deallocate the space for an array, use an empty index: delete[] words

2.3 Container Classes

Container : is a variable that consists of a collection of items.

Container class: is a class whose objects are containers

Two widely used structure for storing items in a container object:

  • Array structure: one of field is the class is an array, the items are stored in this array

    • Advantage: allows random-access of items
    • Drawback: large-scale movement of items for inserting,deleting, and resizing

  • Linked structure: each item has an associated link - a pointer to the next item in the container

    • Define a template,or mold, allow the definition, at compile-time, of container class of some fixed type, let user select the item type when they defines the container object.

    • The container class is a template class, and the given type is a template argument

    • The definition of a template class starts with the template parameter,the type that will be replaced by the template argument when the container object is defined.

    • The Linked class has an embedded iterator class. An Iterator is an object that enables a user to loop through a container without violating the principle of data abstraction.

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      template <typename T>
      class Linked{
      private:
      	struct Node{
      	 		T item;
      	 		Node* next;
      	}
      	Node* head;
      	length;
      public:
      	class Iterator{
      				friend class Linked<T>
      				private:
      					Node* nodePtr;
      				protected:
      					Iterator(Node* newPtr)  // is protected becasue users know nothing node.
      				public:
      				bool operator== const;
      				bool operator!= const;
      				T& operator*() const;
      				bool operator++(int); // post-increment operator
      	}
      	Linked();
      	long size();
      	void push_front(const T& newItem);
      	void pop_front();
      	bool empty();
      	Iterator begin();
      	Iterator end();
      }

  • Destructors

    • A destructor is a method that deallocates the space occupied by an object.
    • No return type, no parameters !
    • The destructor for an object is automatically called when the object goes out-of-scope, that is, when the object is no longer accessible.
    • If a class does not explicitly define a destructor, the compiler will automatically provide one. this default destructor simply calls the destructor for each object field.
    • We had to explicitly define a destructor for the class without object fields to avoid the possibility of a massive memory leak.

2.4 Generic Algorithms

  • A iterator in a class that supports those operators(==,!=,++,*) is called an input iterator.

  • Template functions, also called generic algorithms, constitute one of the three major components of the Standard Template Library.

  • The other two essentials are Container classes and Iterators

  • These connection: Generic algorithms operate on containers through iterators.

3. Time Complexity

3.1 Software Engineering

  • MOORE’S Law: computer power(circuits per chip) doubles about every 18 months.
  • Software engineering: A systematic approach to the development of medium-to-large programs
  • Software-development-life cycle
    • Stage I : Problem analysis
    • Stage II: Program Design
    • Stage II: Program Implementation
    • Stage IV: Program
  • Modification due to
    • errors found
    • enhancements made
    • change in computing environment

3.2 Execution-time Complexity

  • Execution-time requirements: number of statements executed in a trace of the method,given a function of n, the problem size.
  • worstTime(n): the maximum number of statements executed in a trace.
  • averageTime(n): the average number of statements executed in a trace.
  • Maximum and average are over all possible traces of the method,for all possible field, parameter, and input values

3.3 Big-O

  • Definition of big-O

    • Let g be a function that has non-negative integer arguments and returns a non-negative value for all arguments.

    • Define o(g),the order of g, to be the set of functions f such that for some pair of non-negative constants c and k,
      $$
      f(n)<=c \ g(n) \ \ \ for \ all \ \ n >=k
      $$

    • Say f is O(g) ,”f id O of g”,f is eventually less than or equal to some constant time g. So g can be viewed as an upper bound for f.

  • 极限定义

    • 一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用f(n)表示，若有某个辅助函数g(n),使得当n趋近与无穷大时，g(n)/f(n)的极限值为不等于0的常数，则称g(n)是f(n)的同量级函数。
    • 记作f(n)=O(g(n))，称O(g(n))为算法的渐进时间复杂度，简称为时间复杂度

  • Smallest upper bound : o(g) is the smallest upper bound of f that f is o(g) and for any function h, if f is o(h), then
    $$
    o(g) \subset o(h)
    $$

  • Growth Rates

    execution

  • Examples

    1
    2
    3
    4
    5
    for(int i=8;i<n-2;i++){
    	cout << j*j << endl;
    	if(n/2 > j)
    		cout << j*n << endl;
    } // O(n)
    1
    2
    3
    while(n>1){
    	n = n/2;
    } // O(log n)
    1
    2
    3
    4
    5
    6
    for (int j=0;j<n;j++){}
    	cout << (j*j) << endl;
    }
    while(n>1){}
    	n/=2;
    }// O(n)
    1
    2
    3
    4
    5
    6
    for(int j=0; j < n; j++){
    	int temp = n;
    	while(temp > 1){
    		temp = temp/2;
    	}
    } // O(nlogn)
    1
    2
    3
    for(int i=0; i*i < n; i++){
    	cout << i << endl;
    } // O(n^1/2)
    worstTime(n) Smallest upper bound
    Constant O(1)
    logarithmic in n O(log n)
    linear in n O(n)
    quadratic in n O(n^2)

  • Method - estimate conventions(公约)

    • n = number of items in the container
    • If no estimate of worstTime(n) given , worstTime(n) is constant
    • If no estimate of averageTime(n) given, o(averageTime(n)) = o(worstTime(n))

3.3 Run Time Analysis

  • time(null) : return the number of seconds elapsed since midnight on january 1,1970

  • The skeleton of a timing program

    1
    2
    3
    4
    5
    6
    7
    8
    9
    long start_time,
    			finish_time,
    			elapsed_time;
    start_time = time(NULL);
    /*
    	Perfrom Task 
    */
    elapsed_time = finish_time - start_time; // Calculate elapsed time for the task
    cout <<  elapsed_time << endl;

3.4 Randomness

  • Random number: A number is selected randomly from a collection of numbers if each number has an equal chance of being selected.

  • rand() : defined in stdlib.h , returns a “random” int

  • seed: an unsigned int used in the calculation of the value returned by rand()

    1
    2
    3
    4
    srand(100);
    for(int i=0;i<10;i++){
    	cout << rand()%4 << " ";
    } // Random number

4. Recursion

A function is recursive if it include a call to itself

基本形式:

1
2
3
4
if simplest case
	Sovle directly
else 
	Make a recursive call yo simpler case

Consider recursion when :

  • simplest case(s) can be solved directly
  • complex cases can be solved in terms of simpler cases of the same form.

Any problem that can be solved recursively can also be solved iteratively

An Iterative functions is one that has a loop statement

4.1 Factorials

  • We can calculate n! with(n-1)!,because
    $$
    n! = n*(n-1)!
    $$

    1
    2
    3
    4
    5
    6
    7
    8
    9
    // Precondition: n>0
    // Postcondition: The values returned is n!
    long factorial(int n){
    	if(n==0||n==1){
    		return 1;
    	}else{
    		return n*factorial(n-1);
    	}
    } //factorial

  • Execution frames

    • Allow to see what happens during the execution of a recursive function

    • is a box with information (such as parameters values) related to one call to the function

      image-20241217112838074

  • Worsttime(n): O(n) – is linear in n

    • the number of loop iterations as a function of n
    • the number of recursive calls as a function of n

  • Worstspace(n): O(n) – is linear in n

    • the number of variables needed in any trace of this function is linear in n.

  • Iterative function

    1
    2
    3
    4
    5
    6
    7
    8
    9
    long factorial(int n){
    	int product = n;
    	if(n==0)
    		return 1
    	for(int i=n-1;i>1;i--){
    		product = product*i;
    	}
    	return product;
    } // function factorial
    • worsttime : O(n)
    • worstspace: O(1)

4.2 Converting from Decimal to Binary

  • We need to print the binary equivalent of n/2 before we print n%2, stop when n=1 or n=0,and output n

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    // Precondition: n>=0
    // Postcondition: The binary equivalent of  n has been printed
    void writeBinary(int n){
    	if(n==0||n==1){
    		cout << n;
    	}else{
    		writeBinary(n/2);
    		cout << n%2;
    	}
    } // writeBinary

  • worsttime(n): O(log n)

  • worstspace(n): O(log n)

4.3 Towers of Hanoi

Given 3 poles (a,b,c) and n disks of increasing size (1,2,3,…,n), move the n disks form pole a to pole b, use pole c for temporary storage.

  • only one disk may be moved at any time
  • no disk may ever be placed on top of a smaller disk
  • the top disk on any pole may be moved to either of the other poles

We will be able to move 4 disks from one pole to another if we are able to figure out how to move 3 disks form one pole to another

  • if n==1, move disk 1 from pole  'a' to pole 'b'
otherwise,
1. move n-1 disks from 'a' to 'c', with 'b' as a temporary
2. move disk n from 'a' to 'b'
3. move n-1 disks from 'c' to 'b', with 'a' as a temporary

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13

    - ```c++
      // Percondition: n>0
      // Postcondition: The steps needed to move n disks from pole orig to pole dest have been written out. Pole temp is used for temporary storage
      void move(int n, char orig,char dest,char temp){
      	if(n==1){
      		cout  << "Move disk 1 from " << orig << "to " << dest << endl;
      	}else{
      		move(n-1,orig,temp,dest);
      		cout << "Move disk " << n << "from " << orig << "to " << dest << endl;
      		move(n-1, temp , dest, orig);
      	}
      } // move

  • worsttime
    $$
    worsttime(n) \approx O(2^{n})\
    because\ 2^{n}-1 \ disks must be moved
    $$

4.4 Backtracking

Backtracking is the strategy of trying to reach a goal by a sequence of chosen positions, with re-tracing in reverse order of position that cannot lead to the goal.

  • General-Purpose Backtrack Class – Application.h

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    class Application{
    	friend ostream& operator <<(ostream& stream, Application& app);
    		public:
    			Position generateInitialState();
    			bool valid(const Positon& pos);
    			void record(const Positon& pos);
    			bool done(const Position& pos);
    			void undo(const Position& pos);
    			class Iterator{
    				public:
    					Iterator(const Position& pos);
    					Position operator++(int);
    					bool atEnd();
    				protected:
    					void* fieldPtr;
    			} // class Iterator
    	} // class Application

  • BackTrack class

    1
    2
    3
    4
    5
    6
    7
    class BackTrack{
    	protected: 
    		Application app;
    	public:
    		BackTrack(const Application& app);
    		bool tryToSolve(Position pos);
    } // class BackTrac

    The tryToSolve method first constructs an iterator from pos and then loops until success has been achieved or no more iterations are possible.

    Ecah loop iteration considers three possibilities for the new position generated by the iterator

    • goal reached, return true
    • valid position but not the goal; then call tryToSolve to see if success is possible from the current value of pos.
    • invalid position and iterator at end, return false
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    class BackTrack::tryToSolve(Position pos){
    	bool success = false;
    	Application::Iterator itr(pos);
    	while(!success && !itr.atEnd()){
    		pos = itr++;
    		if(app.valid(pos)){
    			app.record(pos);
    			if(app.done(pos)){
    				return true;
    			}else{
    				sucess = tryToSolve(pos);
    				if(!success)
    					app.undo(pos);
    			} // not done
    		} // a valid position
    	} // while
    	return success
    }// method tryToSolve

  • main function

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    Application app;
    Backtrack b(app);
    Position start = app.generateInitialState();
    if(!app.valid(start)){
    	cout << FAILURE << endl;
    }else{
    	app.record(start);
    	if(app.done(start) || b.tryToSolve(start)){
    	cout << SUCCESS << endl << app;
    	}else{
    		app.undo(start);
    		cout << FAILURE  << endl;
    	}// failure
    }// start is valid

  • Maze Problme

    Position calss

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    class Position{
    	public:
        	position();
        	Positon(int row, int column);
        	void setPosition(int row, int column);
        	int getRow();
        	int getColumn();
        protected:
        	int row,
        		   column;
    }// class Positioin
    1
    2
    3
    struct itrFields{
    		int row, column, direction;	
    }

    Iterator constructor

    1
    2
    3
    4
    5
    6
    7
    Application::Iterator::Iterator(Position pos){
    	iterFields* itrPtr = new itrFields;
    	itrPtr->row = pos.getRow();
    	itrPtr->column = pos.getColumn();
    	itrPtr->direction = 0;
    	fieldPtr = itrPtr;
    } //constructor

    operator++(int)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    Position Application::Iterator::operator++(int){
    	itrFields* itrPtr = (itrFields*)filedPtr;
    	int nextRow  = itrPtr->row, nextColumn = itrPtr->columnl
    	switch(itrPtr->direction++){
    		case 0: 
    			nextRow = itrRow->row-1; // north
    			break;
    		case 1:
    			nextColumn - itrPtr->Column+1; // east
    			break;
    		case 2: 
    			nextRow = itrPtr->row+1; // south
    			break;
    		case 3:
    			nextColumn = itrPtr->column-1; // west
    	} // switch
    	Positioin next(nextRow, nextColumn);
    	return next;
    }// operator++(int)

4.5 Searching an Array

  • Generic algorithm find – worsttime: O(n)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    template <class InputIterator, class T>
    InputIterator find(InputIterator first, InputIterator last , const T& value);{
    	while(first  != last && *first != value){
    		++ first;
    		return first;
    	}
    }

    int main(){
        // Find by pointer
        string words[20];
        string* wordPtr = find(words ,words+20, myWord);
        cout << myWord;
        if(wordPtr!=words+20){
           cout <<  "at index" << (wordPtr - words) << endl;
        }else{
            cout << "Not Found." << endl;
        }
        // Find by Linked：：Iterator
        Linked<int> myLinked;
        Linked<int>::Iterator it;
        itr = find(myLinked.begin(),myLinked.end(),someInt);
        if(itr != myLinked.end()){
            cout << "Found" << endl;
        }else{
            cout << "Not Found" << endl;
        }
    }

  • Binary Search – worsttime(n) – O(log n)

    During each iteration, the size of the subarray searched is divided by 2 until success or failure occurs

    basic strategy
    $$
    \begin{aligned}
    & t^{} \ miidle =\frac{ first\ + (last-first)}{2} \
    & if \ ( ^{    }middler < value) \
    & \ \ \ \ search \ from \ middle +1 \ to \ last -1; \
    & else \ if \ (value < \ ^{*}middle ) \
    & \ \ \ \ search \ from \ fisrt \ to \ midlle -1;\
    &else \
    & \ \ \ \ return \ true;
    \end{aligned}
    $$

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    template <typename T>
    bool binary_search(T* first, T* last, const T& value){
    	if(first>=last)
    		return false;
    	T* middle = (first+last)/2;
    	if(*middle < value){
    		return binary_seach(middle+1,last,value);
    	}else if(value < *middle){
    		return binary_search(first,middle,value);
    	}
    	return true;
    }

5. Vector and Deques

The vector, deque , and list classes are sequential-container classes: the items are stored in succession, from first to last.

5.1 Vector

The vector class is a “smart” array:

  1. random-access is supported with the index operator,[];
  2. there is a size method to keep track of the number of items;
  3. re-sizing is automatic
  4. there are methods to insert and delete at any position;
  5. there is an assignment operator to copy a vector to another vector;
  6. the vector class is templated , so you can restrict the type of items for a vector container;
  7. vector are as efficient as arrays

There are 32 methods in the vector class.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
template <typename T>
class vector{
    private:
    	T* finsh;
    	T* start;
    	T* end_of_storage;
	public:
		vector();
		vector(const vector<T>& x);
		// postcondition: this vector object is empty, and will hold up n items before resizing takes place.
		vector(unsigned n);
		vector<T>& operator=(const vector<T>& x);
		// postcondition: x has been inserted at position, and items that were at position or higher have been moved up.
		push_back(const T& x);
		iterator insert(iterator position, const T& x);
		pop_back();
		void erase(iterator position);
		void erase(iterator first, iterator last);      
    	iterator begin();
    	iterator enf();
    	unsized size(){return finish - start;}
    	bool emplty(){return start == finish;}
    	class iterator{}
}

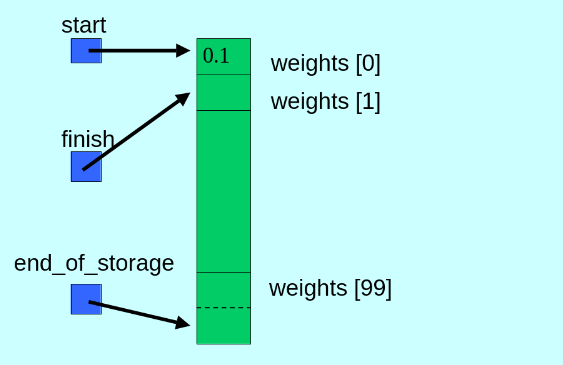
Three pointer fields

  • start: with the address of the 0th location in the array;

  • finish: which points to the location just after the back item of the vector

  • end_of_storage: which points to the location just after the last location allocated for the array.

    image-20241218132119866

  • Insert method

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    iterator insert(iterator position, const T& x)
    {
    	size_type n = position - begin();
    	if(finish != end_of_storage)
    	{
    		if(position == end())
    		{
    			construct(finish,x);
    			finish++;
    		}
    		else
    		{
    			construct(finish,(*finish-1));
    			copy_backward(position,finish-1,finish);
    			*position = x ;
    			++finish;
    		}
    	}
    	else
    	{
    		size_type len = size()? 2*size(): static_allocatior.init_page_size();
    		iterator tmp = static_allocator.allocate(len);
    		uninitialized_copy(begin(),position,tmp);
    		construct(tmp+(position-begin()),x);
    		uninitialized_copy(position,end(),tmp+(position-begin())+1);
    		destroy(begin(),end());
    		static_allocator.deallocate(begin());
    		end_of_storage = tmp + len
    		finish = tmp + size() +1;
    		start = tmp;
    	}
    	return begin() + n;
    }

  • 基本使用

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    int main(){
    vector<string> words;
    string word;
    for(int i=0; i<5; i++)
    {
    	cin >> word;
    	words.push_back(word);
    } // reading in words 
    words.erase(words.begin());
    words.pop_back();
    for(unsigned i=0; i<words,size(); i++)
    {
    	cout << words[i] << endl;
    }
    }

5.2 High-Precision Arithmetic

The class very_long_int to support high-precision arithmetic

1
2
3
4
5
6
class very_long_int
{
	// precondition: the input starts with a sequence of digits, followed by an 'X' , with blanks ,end-of-line markers, and invalid characters ignored. There are no leading zeroes , except for '0' itself.
    // postcondition: very_long contains the very_long_int whose digits came from instream, and a refrerence to instream has been returned .
	friend istream& operator>>(istream& instream , very_long_int& very_long);
}

5.3 Deques

6. Lists

A list, sometimes called a linked list, is a finite sequence of items such that:

  • accessing or modifying an arbitrary item in the sequence takes linear time;

  • given an iterator at position in the sequence, inserting or deleting at that position takes constant time.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    int main()
    {
    	List<string> words;
    	List<string>::Iterator itr;
    	for(int i=0; i<5; i++)
    	{
    		word = (char)(i+'a');
    		words.push_back(word);
    	} // for
    	itr = words.begin();
    	itr++;
    	itr++;
    	words.insert(itr,"true");
    	itr = words,insert(itr,"good");
    	words.insert(itr,"right");
    	for(itr = words.begin(); itr!=words.end();itr++)
    		cout << *itr << endl;
    }
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    template <typename T>
    class List{
    	private:
    		struct List_node{
    			List_node* next;
    			List_node* prev;
    			T data;
    		} // List_node
    	protected:
    		unsigned node;
    		list_node* head;
    	public:
    		classs Iterator{
    			friendly class List<T>;
    			protected: 
    				list_node* node;
    				Iterator(list_node* x): node(x){}
    			public:
    				Iterator& operator--();
    		}
    		Iterator push_pront(const T& item);
    		Iterator push_back(const T& item);
    		void pop_front();
    		void pop_back();
    		bool empty();
    		int size();
    		Iterator begin();
    		Iterator end();
    		Iterator insert(Iterator position, const T& item);
    		void erase(Iterator position);
    		void erase(Iterator first, Iterator last); // [frist, last)		
    		void splice(Iterator position, List<T>& x); // insert x befroe position	
    		void sort();
    }
    template <typename T>
    List<T>::Iterator List<T>::Iterator::operator--(){
    	node = node->prev;
    	return *this;
    }
    template <typename T>
    List<T>::Iterator List<T>::insert(Iterator position, const T& item)
    {
    	List_node* temp = new List_node;
    	temp->data = item;
    	temp->next = position->next;
    	temp->prev = position->prev;
    	postion->prev->next = temp;
    	position->prev = temp;
    	++length;
    	return temp;
    }

    ​ image-20241220170251809

7. Queue & Stacks

7.1 Queue

8.Binary & Search Tree

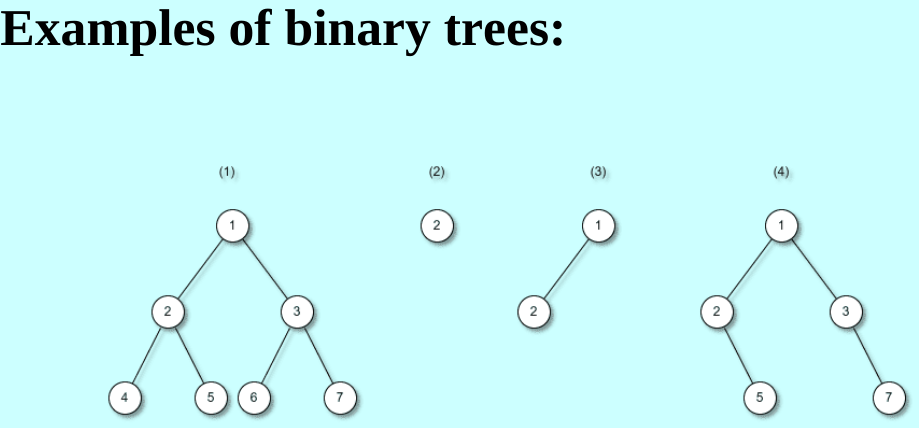
8.1 Binary Trees

A binary tree t is either empty or consists of an item, called the root item, and two distinct binary trees, called the left subtree and right subtree of t.

  • Empty

  • Only root (with two empty child)

  • less than or equal to 2 childs

    image-20241225095137042

Terminology

  • Leaf : an item whose left and right subtrees are empty

    • define the number of leaf

      1
      2
      3
      4
      5
      6
      if t is empty
      	leaves(t) = 0
      else if t consists of a root item only
      	leaves(t) = 1
      else 
      	leaves(t) = leaves(leftTree(t))+leaves(rightTree(t))

  • branch : a line drawn from an item to its left and right subtree

  • expression tree : each leaf is an operand, and each non-leaf is operator

  • binary search tree

    • each item in the left subtree is less than the root item
    • each item in the right subtree is greater than the root item
    • the left and right subtree are themselves binary search tree

  • descendant : the item’s child’s child … is the item’s descendant

  • path : a sequence of items in which each item except the last , is the parent of the next item in sequence.

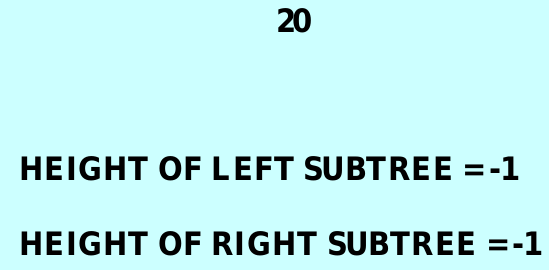
  • height(t) : the number of branches from the root to the farthest leaf

    • define the method counting height

      1
      2
      3
      4
      5
      if t is empty
      	height(t) = -1;
      else
      	height(t) = max(heigt(leftTree(t)),height(rightTree(t))) + 1;

  • depth(x) / level(x) : the depth of an item x is the number of branches from the root to x

    • define the number of depth(x)
    1
    2
    3
    4
    if x is the root item
    	depth(x) = 0
    else 
    	depth(x) = depth(parent(x)) +1

  • two-tree

    • a biif\ t\ is\ full\ , nary tree t is two - tree if t is empty or if each non-leaf in t has two branches

    • Recursively speaking

      a binary tree t is a two-tree if t is empty or if leftTree(t) and rightTree(t) are either both empty or both non-empty two-trees.

  • full-tree

    • binary tree t is full if t is a two-tree and all of the leaves of t have the same depth

    • Recursively speaking

      a binary tree t is full if t is empty or if height(leftTree(t)) = height(rightTree(t)) and both leftTree(t) and rightTree(t) are full trees.

  • complete tree

    • a binary tree t is complete if t is full through a depth of height(t)-1, and each leaf whose depth is height(t) as far less to left as possible
    • a complete binary tree can be stored in an array

  • The binary-tree theorem – n(t) 节点数量

    • $$
      leaves(t) <= \frac{n(t)+1}{2.0}
      $$

    • $$
      \frac{n(t)+1}{2.0} <= 2^{height(t)}
      $$

    • $$
      if\ t \ is\ a\ two\ tree\ ,\ leaves(t) = \frac{n(t)+1}{2.0}
      $$

    • $$
      if\ leaves(t) = \frac{n(t)+1}{2.0}, t\ is a two \ tree
      $$

    • $$
      if\ t\ is\ full\ , \ \frac{n(t)+1}{2.0} = 2^{height(t)}
      $$

    • $$
      \ \frac{n(t)+1}{2.0} = 2^{height(t)} , \ if\ t\ is\ full\ ,\
      height(t) = log_2(\frac{n(t)+1}{2.0})
      $$

    • The average time to insert, remove , search is logarithmic in n

8.2 External Path

Let t be a non-empty binary tree. e(t), the external path length of t, is the sum of the depths of all leaves in t.

The external path length theorem : let t be binary tree with k>0 leaves. then
$$
E(t) >= (k/2)floor(log_2k)
$$

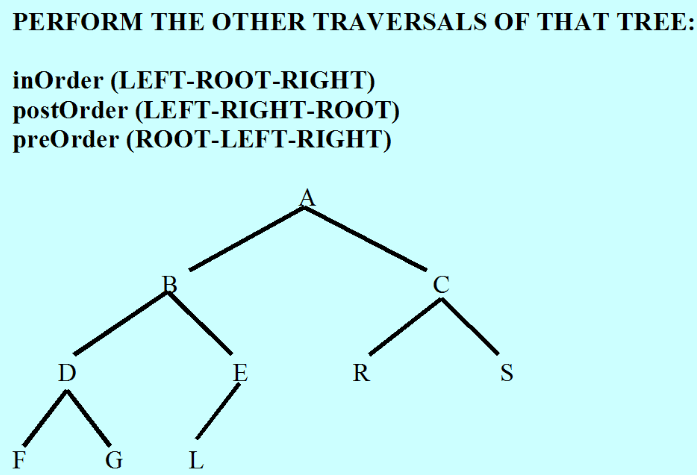
8.3 Traversals of a binary tree

  • inOrder Left-Root-Right

    1
    2
    3
    4
    5
    6
    7
    8
    9
    inOrder(t)
    {
    	if(t is not empty)
    	{
    		inOrder(leftTree(t));
    		access the root item of t;
    		inOrder(rightTree(t));
    	}//if
    }// inOrder traversal

  • postOrder Left-Right-Root

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    postOrder(t)
    {
    	if(t is not empty)
    	{
    		postOrder(leftTree(t))
    		postOrder(rightTree(t))
    		acess the root item  of t;
    	}// if
    }// postOrder traversal

  • preOrder(t) Root - Left - Right

    1
    2
    3
    4
    5
    6
    7
    8
    9
    preOrder(t)
    {
    	if(t is not empty)
    	{
    		access the root item of t;
    		preOrder(leftTree(t));
    		preOrder(rightTree(t));
    	}//if
    }// preOrder traversal

    access

8.4 Binary Search Trees

A binary search tree need not be full, complete or a two-tree, but it could be any of those. If a binary search tree is full or complete, its height is logarithmic in n.

The binary Tree class is an associative-container class , the location of an item is determined by comparing the item to items already in there .

The method interface for an minimal Binary Search Tree class:

bst

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
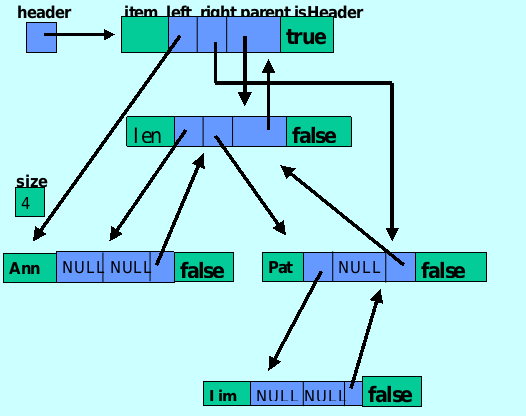
template <typename T>
class BinSearchTree
{
	private:
		struct tree_node
		{
			T item;
			tree_node* parent;
			tree_node* left;
			tree_node* right;
			bool isHeader;
		};// tree_node
	tree_node* header;
    unsigned node_count;
	publlic:
		class Iterator
		{
			protected:
				typedef tree_node* Link;
				Link link;
				Iterator(Link new_link):link(new_link){}
		}
		BinSearchTree(){
			header = new tree_node;
			header->parent = NULL;
			header->left = header;
			header->right = header;
			header->isHeader = true;
			node_count = 0;
		}; // default constructor
		unsigned size()const
        {
            return node_count;
        }
		Iterator find(const T& item)const;
		Iterator insert(const T& item);
		void erase(Iterator itr)
		Iterator begin()
        {
            return header->left;
        }
		Iterator end()
        {
            return header;
        }
		~BinSearchTree();
}

Use example

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <bst_.h>
using namespace std;
int main()
{
	BinSearchTree<string> words;
	BinSearchTree<string>::Iterator itr1;
	string word;
	cin >> word;
	while(word != '***')
	{
		words.insert(word);
		cin>> word;
	}
	for(itr1 = words.begin();itr1 != words.emd(); itr1++)
	{
		cout << *itr1 << endl;
	}
	words.erase(words.find('maybe'));
	words.erase(words.begin());
	words.erase(words.end());
	words.erase(--words.end());
	for(itr1 = words.begin();itr1 != words.end();itr1++)
	{
		cout << *itr << endl;
	}
	return 0;
}

Find method: – O(log n)

  • a child pointer starts at the root, a parent pointer starts at the root, and a parent pointer starts at the header.

  • a loop descends the tree

  • if child's item >= item sought, child is replaced with the left child，and parent is replaced with child

  • otherwise, child is replaced with its right child.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    Iterator find(const T& item)
    {
    	Link parent = header;
    	Link child = header->parent;
    	while(child!=NULL)
    	{
    		if(!(child->item<item))
    		{
    			parent = child;
    			child = child->right;
    		}
    		else
    		{
    			child = child->right;
    		}
    		if(parent == header || item< parent->item)
    			return end();
    		else
    			return parent;
    	}
    }//find

The Insert method:

  • The item is inserted in a tree node to the left or right of parent

  • The header node’s left or right field is updated if the item is smallest or largrst

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    Iterator insert(const T& item)
    {
    	if(header->parent == NULL)
    	{
    		insertLeaf(item,header,header->parent);
    	}//inserting at tree's root
    	else
    	{
    		Link parent = header;
    		Link child = header->parent;
    		child(child!=NULL)
    		{
    			parent = child;
    			if(item < child->item)
    			{
    				child = child -> left;
    			}
    			else
    			{
    				child = child->right;
    			}
    		}// while
    		if(item<parent->item)
    		{
    			insertLeaf(item,parent,parent->left);
    			if(header->left==parent)
    				header->left = parent->left;
    			return parent->left;
    			}//insert at left of parent
    			else
    			{
    				insertLeaf(item,parent,parent->right);
    				if(header->right == parent)
    					header->right = parent -> right;
    				return parent->right;
    			}//insert at right of parent
    	} // tree is not empty
    }//insert

    void insertLeaf(const T& item,Link parent,Link& child)
    {
        child = new tree_node;
        child->item = item;
        child->parent = parent;
        child->left = NULL;
        child->right =NULL;
        child->isHeader = false;
        node_count++;
    }//insertLeaf

The delete method

  • To delete the node that itr is position at, we need to make an adjustment to the parent of that node

    1
    2
    3
    4
    5
    6
    7
    8
    9
    void erase(Iterator itr)
    {
    	if(itr.link->parent->parent == itr.link) // itr at root node
    		deleteLink(itr.->parent->parent)
    	else if(itr.link->parent->left = itr.link)
    		deleteLink(itr.link->parent->left);
    	else
    		deleteLink(itr.link->parent->right);
    }//erase
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    void deleteLink(Link& link)
    {
    	if(link->left == NULL || link->right == NULL) // non or only one child
    		prune(link);
    	else if(link->right->left==NULL) // 右孩子的左孩子为空
    	{
    		link->item = link->right->item;
    		prune(link->rigth);
    	}// link's right subtree has an empty left subtree
    	else // 右孩子的左孩子不为空
    	{
    		Link temp = link ->right -> left;
    		while(temp->left != NULL)
    			temp = temp -> left;
    		link->item = temp->item;
    		prune(temp->parent->left);
    	}// link's right subtree has a nonempty left subtree
    }// deleteLink
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    void prune(Link& link)
    {
    	Link linkCopy = link;
    	Link newLink;
    	node_count--;
    	if((link->left == NULL)&&(link->right==NULL))
    	{
    		if(link==header->left)
    			header->left = link->parent;
    		if(link==header->right)
    			header->right = link->parent;
    		link= NULL;
    	}//link 的项是树叶
    	else if(link->left == NULL)
    	{
    		link = link->right;
    		link->parent = linkCopy->parent;
    		if(linkCopy==header->left)
    		{
    			newLink = link
    			while(newLink->left!=NULL)
    				newLink = newLink->left;
    			header->left = newLink;
    		}
    	}//link->left为空
    	else
    	{
    		link = link -> left;
    		link->parent = linkCopy->parent;
            if(linkCopy == header->right)
            {
            	newLink = link;
            	while((newLink->right)!=NULL)
            		newLink = newLink->right;
            	header->right = newLink;
            }
    	}// link-left非空
    	delete linkCopy;
    }// prune

9. AVL Tree

9.1 AVL Tree

  • A tree-oriented data structure is balanced if its height is logarithmic in n.

    Suppose we have an avl tree of height h with n items
    $$
    n>=min_{h} = fib(h+3) -1 > =(\frac{3}{2})^{h}\
    n>=\frac{3}{2}^{h}\
    h<=\frac{log_2n}{log_2\frac{3}{2}}\
    $$

一共有四种旋转

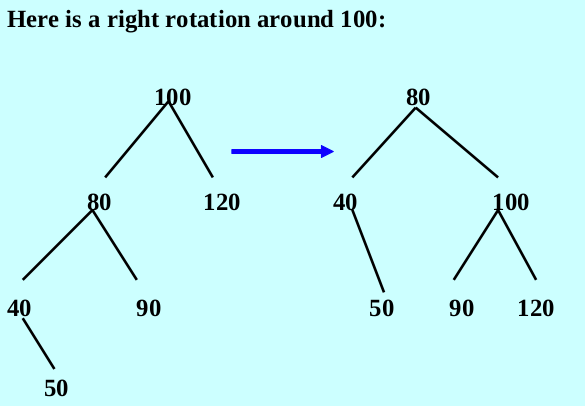
  • 右旋

    • 旋转节点变为旋转节点左孩子的右孩子

    • 旋转节点左孩子的友孩子变成旋转节点**(new)**的左孩子

      avl1

  • 左旋

    • 旋转节点变成旋转节点右孩子的左孩子

    • 旋转节点右孩子的左孩子变为旋转节点**(new)**的右孩子

      avl2

  • 先对需要旋转节点的左孩子左旋，再对需要旋转节点右旋（左旋右旋）

  • 先对需要旋转节点的右孩子右旋，再对需要旋转节点左旋（右旋左旋）

An AVL tree is a binary search tree that either is empty or in which

  • The heights of the left and right subtrees differ by at most 1

  • The left and right substrees are avl trees.

  • Example

    image-20241226173856522
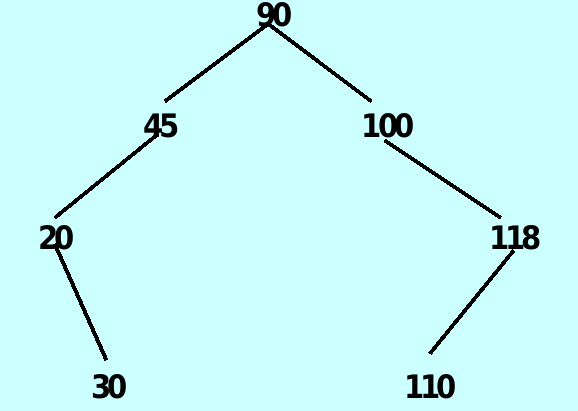
image-20241226173956240

9.2 The AVLTree Class

  • Same as for BinSearchTree Class, but worstTime(n) is O(log n) for find ,insert, and erase 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    template <class T, class Compare>
    Class AVLTree	{
    	private:
        	struct tree_node{
                	T item;
                	tree_node* parent;
                	tree_node* left;
                	tree_node* right;
                	bool isHeader;
                	char balanceFactor;
            }
        	Compare compare;
          	tree_node* header;
        	long node_count;
        	
    	public :
    	// worstTime(n) is constant
    		unsigned size();
    		Iterator begin();
    		Iterator end();
    		
    		// worstTime(n) is O(log n)
    		Iterator find(const T& item);
    		void insert(const T& item);
    		void erase(Iterator position);
    		
    		// worstTime(n) is O(n)
    		~AVLTree();
    }

  • The AVLTree Class allows users determine how to order the node data

    The function class, is a class in which the function call operator, operator(), has been overload.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    // Function class example
    class Sample
    {
    	public:
    		double operator()(int i)
    		{
    			return 1.0/i;
    		}
    }; // class Sample
    class ByLength
    {
        	public:
        		bool operator()(const string& s1, const string& s2)
                {
                    return s1.length() < s2.length();
                }//operator
    }// class ByLength
    template <class T>
    struct less:binary_function<T,T,bool>
    {
    	bool operator()(const T& x, const T& y)const{
    		return x>y;
    	}
    }
    int mian(){
    	Sample f; // f is a function object
    	cout << f(39) << endl; 
    }
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    int main(){
    	AVLTree<string,ByLength> avl1; // 比较字符串长度
    	avl1.insert("yes");
    	avl1.insert("no");
    	avl1.insert("maybe");
    	AVLTree<string,ByLength>::Iteraor itr1;
    	for(itr1 = avl1.begin();itr1!=avl1.end();itr1++)
    	{
    		cout << *itr1 << endl;
    	}
        AVLTree<string,less<string>> avl2; // 比较字母大小
        avl2.insert("yes");
        avl2.insert("no");
        avl2.insert("maybe");
        AVLTree<string,less<string>>::Iterator itr2;
        for(itr2=avl2.begin();itr2!=avl2.end();itr2++)
        {
            cout << *itr2 << endl;
        }
    	return 0;
    }
    /**
    	The output:
    	no yes maybe
    	maybe no yes  
    */

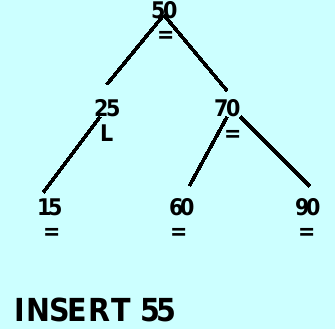
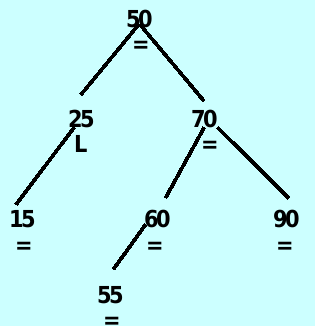
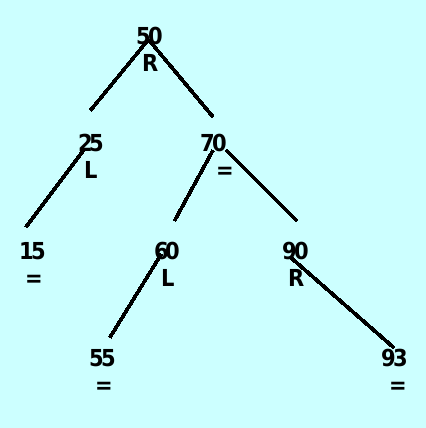
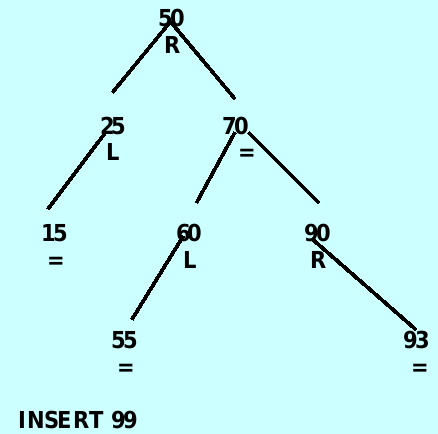
  • The insert method

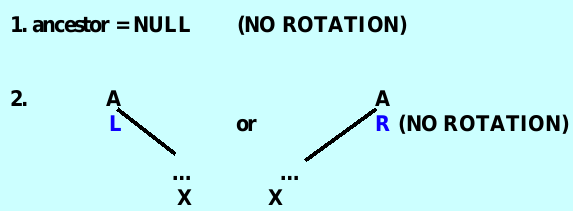
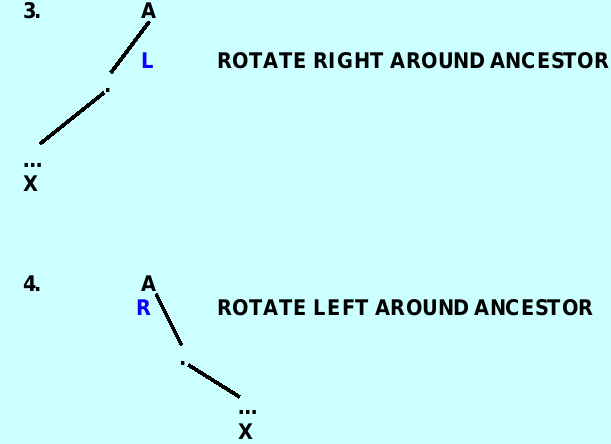
    The ancestor node – has a balanceFactor of ‘L’ or ‘R’ and is closest to where the new item will be added.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    void inser& item)
    {
    	tree_node* parent = header,
    						child = header->parent;
    						ancestor = NULL;
    	while(child!=NULL)
    	{
    		parent = child;
    		if(child->balanceFactor != '=')
    		{
    			ancestor = child;
    			if(compare (item,child->item)) // less(x,y){return x<y}
    				child->child->left;
    			else
    			child = child->right;
    		}
    	}
    	if(compare(item,parent->item))
    	{
    		insertItem(item,parent,parent->left);
    		fixAfterInsertion(ancestor,parent->left);
    		if(header->left == header)
            	header->left = parent->left;
            return parent->left;
    	}
    	else
    	{
    		insertItem(item,parent,parent->item);
    		fixAfterInsertion(ancestor,parent->right);
    		if(header -> right == parent)
    			header->rright == parent->right;
    		return parent->right;
    	}
    }

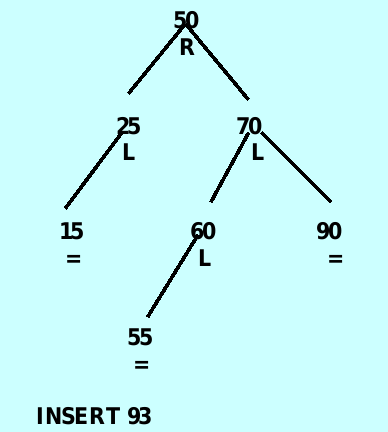
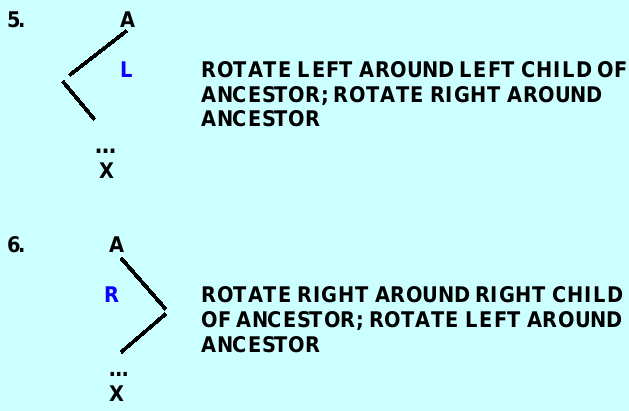
  • SIX cases

    case 1: ancestor is NULL – 直接插入，无需调整

    image-20241226195019098

    case 2: ancestor->balanceFactor is ‘L’ and the insertion was in ancestor’s right subtree – 直接擦插入无需调整

    image-20241226195524032 image-20241226195550162

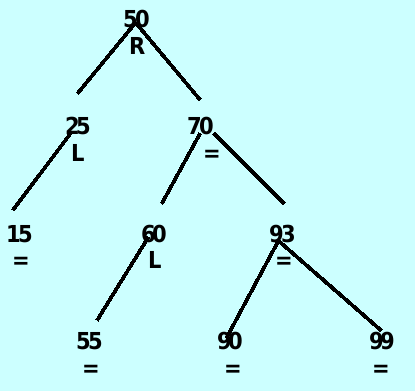
    case 3: ancestor->balanceFactor is ‘R’ and the inserted item is in the right subtree – 正常插入节点后对ancestor 节点进行左旋

    image-20241226200054898

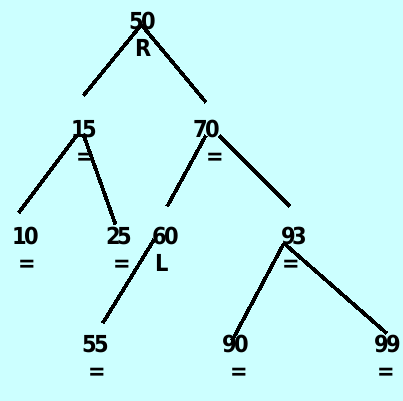
    case 4 : ancestor->balanceFactor is ‘L’ and the inserted item is in the left subtree of the left subtree of ancestor – 正常插入节点后对ancestor 节点进行右选

    image-20241226200404320 image-20241226200423390

  • case 5: ancestor->balanceFactor is ‘L’ and the inserted item in the right subtree of the left subtree of ancestor – 先对ancestor->left 进行左旋，再对ancestor 进行右旋

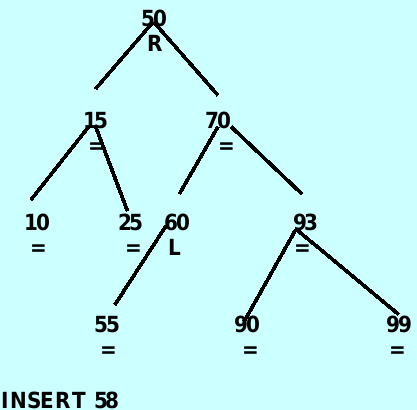
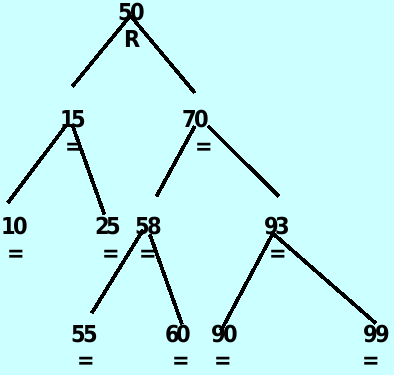
image-20241226201055402 image-20241226201549888

case 6: ancestor->balanceFactor is ‘R’ and the inserted item is in the left subtree’s of the right subtree of ancestor – 先对ancestor->right进行右旋，再对ancestor进行左旋

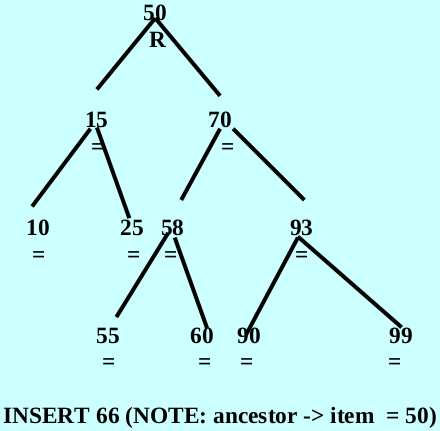
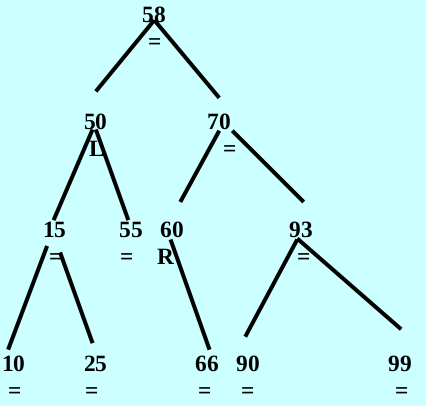
image-20241226201757564 image-20241226202038923

  • Conclusion

    img_6

    image-20241226202224526 image-20241226202316024

9. Red-Black Trees

9.1 Basically definition

A red-black tree is a binary search tree in which the root item is colored black, every other item is colored red or black , and

  • red rule : a red item cannot have any red children

  • path rule : the number of black items is the same in any path from the root item to an item with no children or one child.

  • red-black tree is not a avl tree
    $$
    log_2(n)<=height <= 2log_2(n)
    $$

  • example

    image-20241228195752467

  • The rb_tree class

    two coloring convention:

    • header’s node is red
    • when item is inserted , it is colored red initially

    There is a special node(pointer) NIL

    • NIL’s color_field is black
    • NIL’s left_link and right_link fields are NULL
    • NIL’s parent_link is initially NULL.
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    template <typename Value>
    class rb_tree {
     private:
    		enum color_type = {red,black};
    		struct rb_tree_node
    		{
    			color_type color_field;
    			rb_tree_node* parent_link;
    			rb_tree_node* left_link;
    			rb_tree_node* right_link;
    			Value value_field;
    		}
    public:
    	color_type color(rb_tree_node node);
    	rb_tree_node parent(rb_tree_node node);
    	rb_tree_node root();
    	Iterator insert(const VALUE& v);
    	void erase(Iterator position);
    }

9.2 Insertion Method

There are five steps to accomplish the insertion of the insertion of the item v into an rb_tree object

  • worstTime(n) and averageTime(n) is O(log n)

  • create a node pointed to by x;

  • set value(x) to v;

  • Insert *x as a leaf(with a BinSearchTree-style insertion), and set color(x) to red;

  • Fix up the tree by re-coloring and restructring, if the red rule is violated(path rule ok : red insertion); 最开始调整是因为红色规则违反问题

  • set color(root()) to black

  • The step 4 detail needed

    • Not if x(the node pointed to by x) is the root, because then step 5 will set x’s color to black

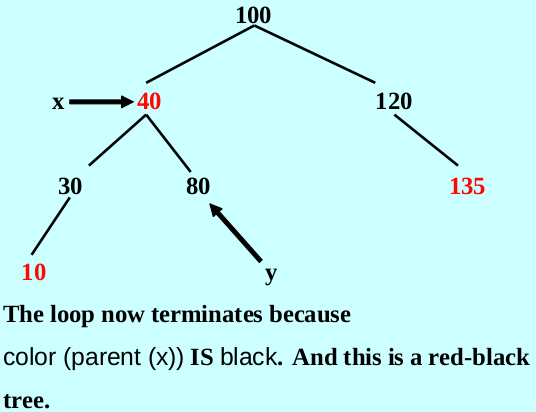
    • if color(parent(x)) is black, then no restructuring is needed because the red rule is not violated

    • parent(x) is left child(action depends on the sibling of parent(x))

      let y be the sibling of parent(x)

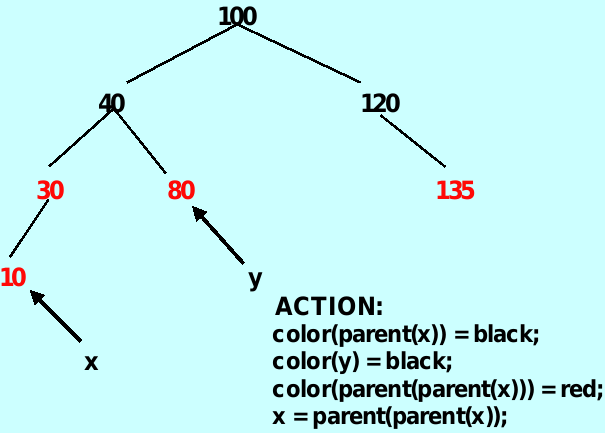
      case 1– color(y)==color_type. red

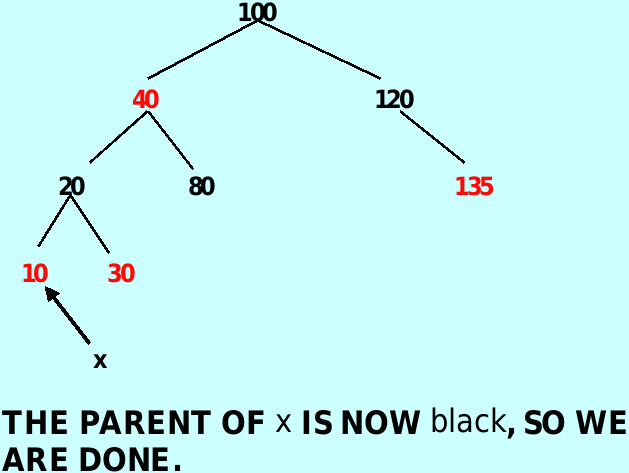
      把插入节点父母和父母的姐妹变成黑色，把插入节点父母的父母变成红色，再把插入节点变成父母的父母的颜色（显示变为红色）

      image-20241228202955226 image-20241228203045327

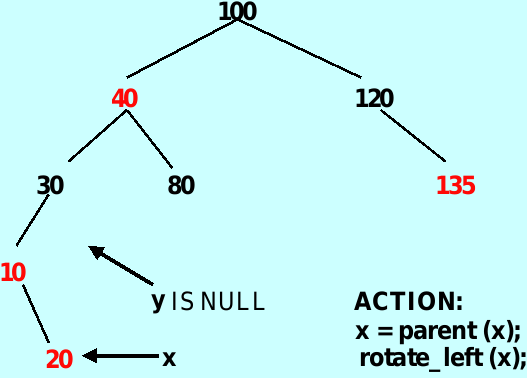
      case 2: color(y) == color_type. black, and x is a right child – y is NIL

      将x（指向插入节点位置的变量）赋值为x的父母，在将x左旋，达到情况3

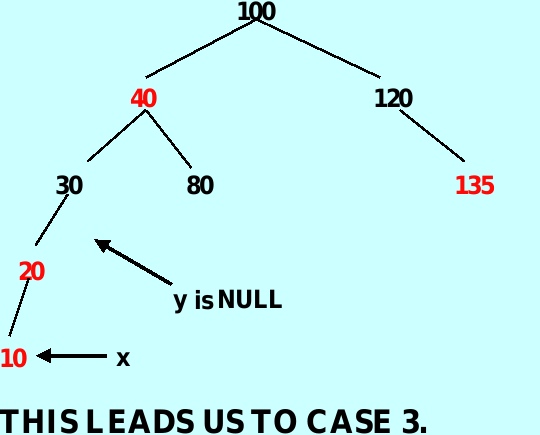
      image-20241229084509396 image-20241229084556529

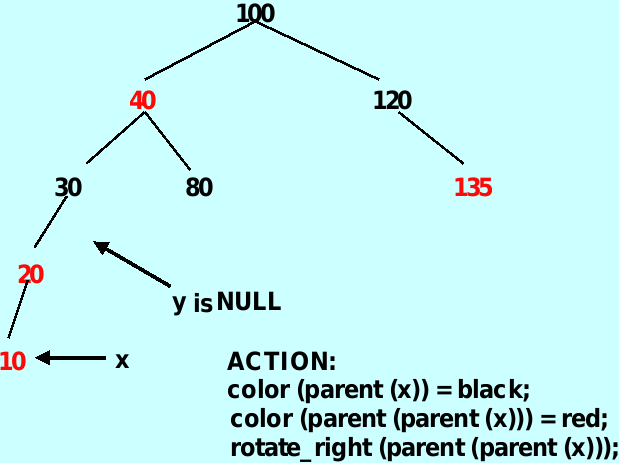
      case 3: color(y) == color_type. black , and x is a left child – y is NIL

      将x（经过case 2 的赋值已经指向原来插入位置的副节点）的父母的颜色赋值为黑色，将x父母的父母的颜色赋值为红色，再右旋x父母的父母

      image-20241229084724680 image-20241229084827684

    • parent(x) is right child(action depends on the sibling of parent(x))

      let y be the sibling of parent(x)

      case 1: color(y) == color_type. red

      把插入节点父母的父母变成红色，把插入节点父母和父母的姐妹变成黑色，把插入几点显示变为与父母的父母相同的颜色

      case 2: color(y) == color_type. black and x is a left child – y is NIL

      将x（指向插入节点的位置），在将x右旋，达到情况3

      case 3: color(y) == color_type. black and x is a right child – y is NIL

      将x的父母赋值为红色，再将x的父母的父母赋值为黑色，x的父母的父母左旋

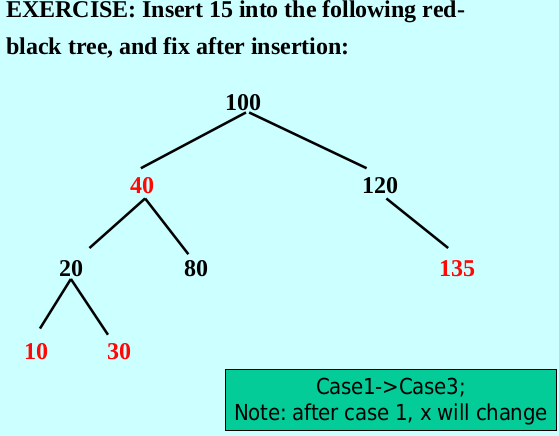
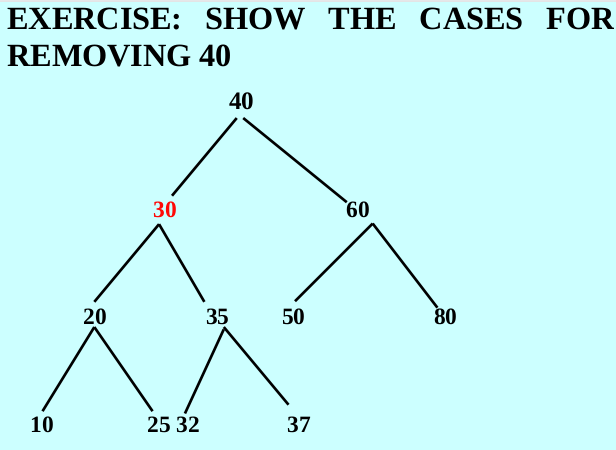
  • Exercise

9.3 Erase Method

It turns out that there is work to be done only if

  • worsTime(n) is O(log n) , averageTime(n) is constant , amortizedtime(n) is constant

  • The deleted node is a black leaf

  • The deleted node has two children and replacement node is a black leaf

  • In either case, the replacement node is itself replaced by a NIL node

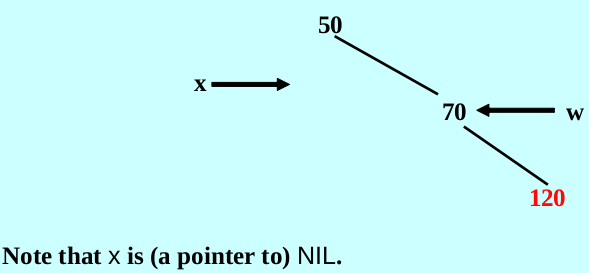
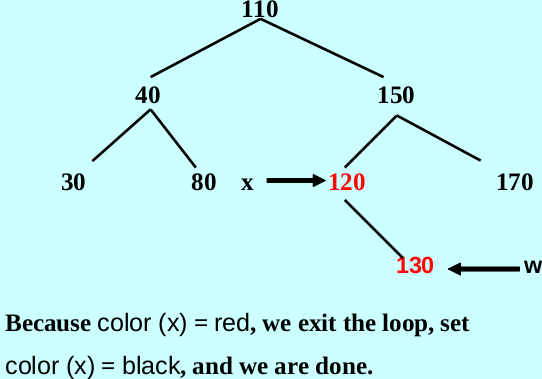
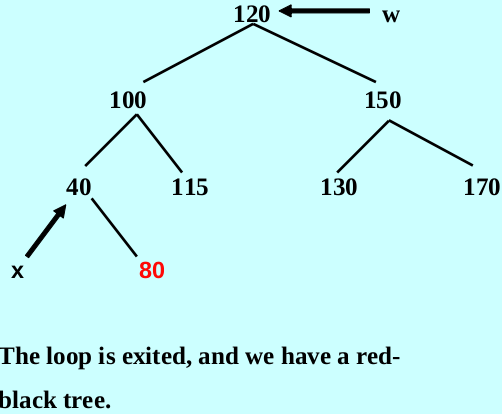
  • Let x be that NIL node, let w be the siblings of x

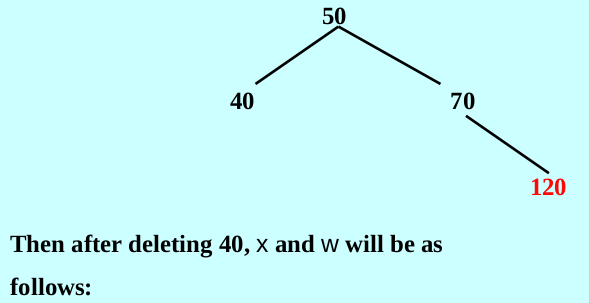
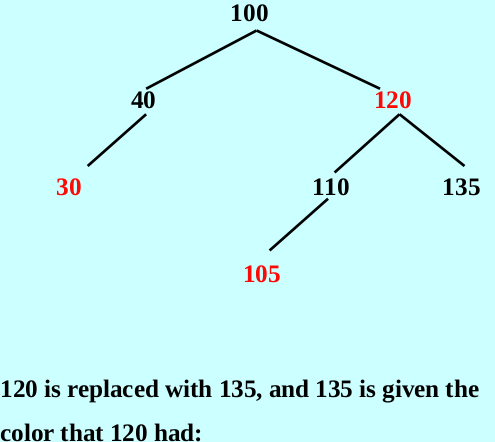
    • Example

      image-20241229091953587 image-20241229092016505

      image-20241229092104759 image-20241229092130367

  • The detail of erase method

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    while(x!=root()&& color(x)==black)
    {
    	if(x==left(parent(x)))
        {
            w = right(parent(x));
            if(w' s color is red) {...case1...};
            if(w' s children are both black) {{....case 2...}}
            else if (right(w) is black ){...case 3 ...}
            else if(righe(w) is red){...case 4 ...}
        }
    }//while
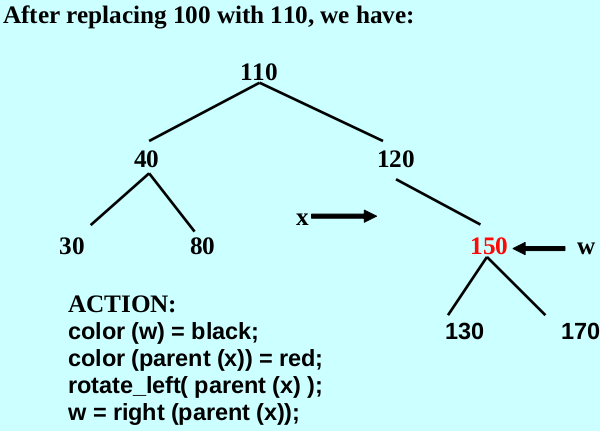
    color(x) = black;

    • when x is a left child

      case 1: color(w) = red

      先找到替代节点位置x，再将w赋值为黑色，x的父母为红色，对x的父母进行左旋，将w赋值为x现在的姐妹节点

      1
      2
      3
      4
      color(parent(x)) = red;
      color(w) = black;
      left_rotated(parent(x)); // x 少了一个左孩子，所以进行左旋
      w = rigth(parent(x));

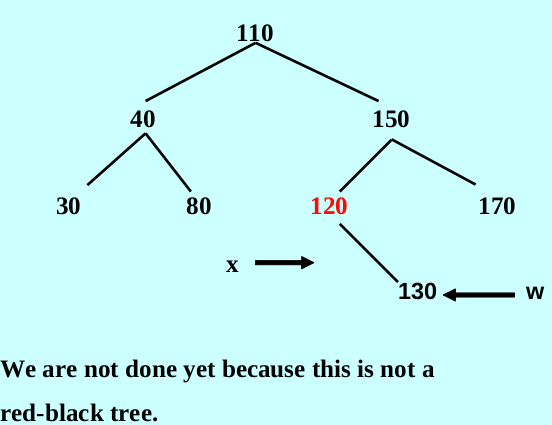
      image-20241229093132386 image-20241229093153305

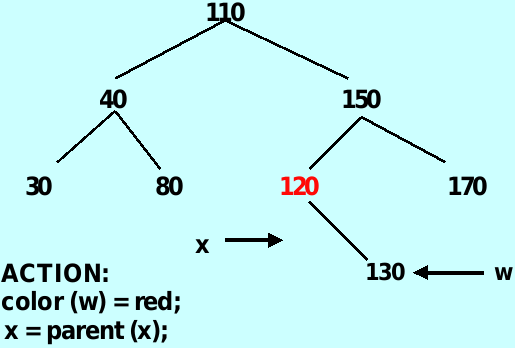
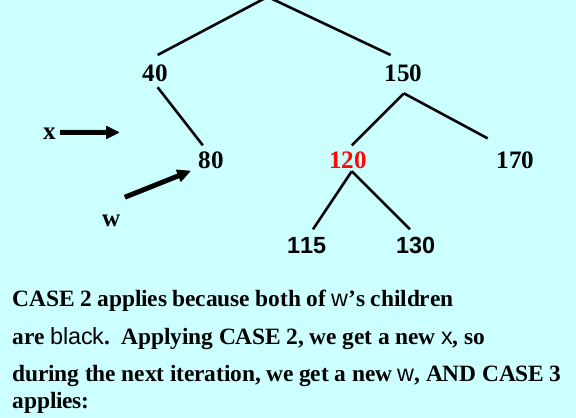
      case 2: color(w) = black and both of w’ s children are black

      case 1 的结果满足这种情况，将w赋值为红色，x赋值到x的父母的位置

      1
      2
      color(w) = red;
      x = parent(x);

      image-20241229094056731 image-20241229094120234

      case 3: color(w) = black and color((right(w))) = black

      如果满足case 2, 先对case 2 进行处理，处理后仍满足case 3， 则将w的左孩子赋值为黑色，再将w的赋值为红色，对w进行右旋，w更新为旋转后x的父母右孩子

      1
      2
      3
      4
      color(w) = red;
      color(left(w)) = color(w);
      right_rotate(w); // left(w)变黑后左边子树更高，因此需要右转
      w = right(parent(x));

      image-20241229095027319

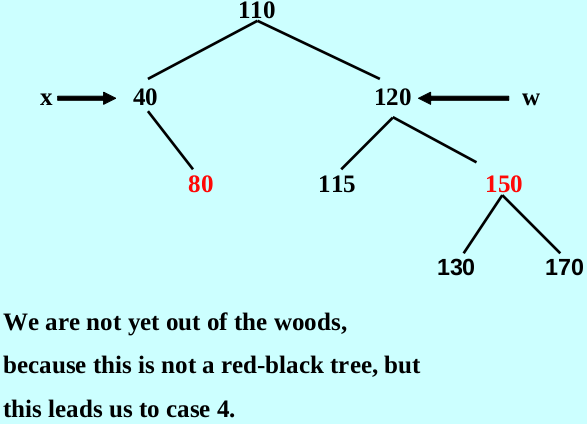
      image-20241229095116280 image-20241229095138273

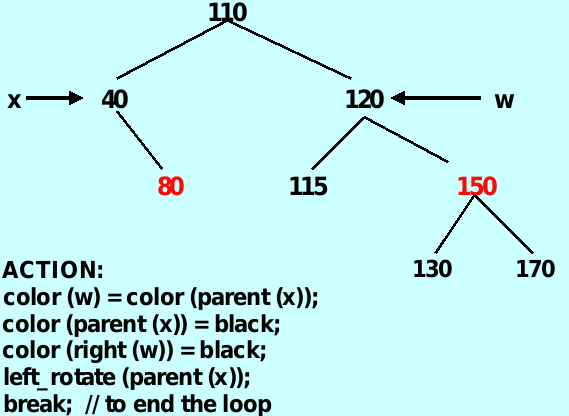
      case 4: color(w) = black ,and color(right(w)) = red

      将w赋值为x父母的颜色，将x的父母的颜色和w右孩子的颜色赋值为黑色，将x的父母左旋，退出循环

      1
      2
      3
      4
      5
      color(w) = color(parent(x));
      color(parent(x)) = black;
      color(right(w)) = black;
      left_rotate(parent(x));
      break;

      image-20241229103135298 image-20241229103208462

      when x is a right child

      case 1: color(w) = red

      先找到替代节点位置x，再将w赋值为黑色，x的父母赋值为红色，对x的父母进行右旋，将w赋值为x现在的姐妹节点

      1
      2
      3
      4
      color(parent(x)) = red;
      color(w) = black;
      right_rotate(parent(x));
      w = left(parent(x));

      case 2: color(w) = black and w’ s children are black

      将w赋值为红色，将x指向x的父母

      1
      2
      color(w) = red;
      x = parent(x);

      case 3: color(w) = black and color(left(w)) = black

      将w赋值为红色，将x的右孩子赋值为黑色，对w进行左旋，再将w更新为旋转后的x的父母的左孩子

      1
      2
      3
      4
      color(left(w)) = red;
      color(right(w)) = black;
      leftr_rotate(w);
      w = left(parent(x));

      case 4: color(w) = black, and color(left(w)) = red

      将w变为w父母的颜色，将w的右孩子和w的父母变为黑色，将w父母（也是x的父母）右旋，退出循环

      1
      2
      3
      4
      5
      color(w) = color(parent(x));
      color(parent(x)) = black;
      color(left(w)) = black;
      right_rotate(parent(x));
      break;

  • Exercise

    image-20241229111340981 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    while(x!=root() && color(x) == black)
    	if(x==left(parent(x)))
    	{
    		link_type w = lef(parent(x)); 
    		if(color(w) == red) // case 1
    		{
    			color(parent(x)) = red;
    			color(w) = black;
    			rotate_left(parent(x));
    			w = right(parent(x));
    		}
    		if(color(right(w))==black && color(left(w))==black) // case2
    		{
    			color(w) = red;
    			x = parent(x);
    		}
    		else 
    		{
    			if(color(right(w))==black) // case 3
    			{
    				color(left(w))=black;
    				color(right(w)) = red;
    				rotate_right(w);
    				w = rigth(parent(x));
    			}
    			else // case 4
    			{
    				color(w) = color(parent(x));
    				color(parent(x)) = black;
    				color(right(w)) = black;
    				rotate_left(parent(x));
    				break;
    			}
    		}
    	}else{
    		link_type w = left(paren(x));
    		if(left(w)==red)
    		{
    			color(w) = black;
    			color(parent(x)) = red;
    			rotate_right(parent(x));
    			w = left(parent(x));;
    		}
    		if(color(right(w))==black && color(left(w))==black)
    		{
    			color(w) = red;
    			x = parent(x);
    		}else{
    			if(left(w)=black)
    			{
    				left(w) = red;
    				right(w) = black;
    				rotate_left(w);
    				w = left(parent(w));
    			}else
    			{
    				color(w) = color(parent(x));
    				color(parent(x)) = black;
    				color(left(w)) = black;
    				rotate_right(parent(x));
    				break;
    			}
    			color(x) = black;
    		}
    	}
  • Title: DataStructure
  • Author: Francessca
  • Created at : 2024-12-29 11:44:03
  • Updated at : 2024-12-29 14:26:32
  • Link: https://francesscawy.github.io/2024/12/29/DataStruture/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
DataStructure
  1. 1. Class in C++
    1. 1.1 Data Structure
    2. 1.2 Class in C++
    3. 1.3 Principle of data abstraction
    4. 1.4 The open-closed principle
    5. 1.5 Subclass substitution rule
  2. 2. Container Classes
    1. 2.1 Dynamic variable
    2. 2.2 Arrays
    3. 2.3 Container Classes
    4. 2.4 Generic Algorithms
  3. 3. Time Complexity
    1. 3.1 Software Engineering
    2. 3.2 Execution-time Complexity
    3. 3.3 Big-O
    4. 3.3 Run Time Analysis
    5. 3.4 Randomness
  4. 4. Recursion
    1. 4.1 Factorials
    2. 4.2 Converting from Decimal to Binary
    3. 4.3 Towers of Hanoi
    4. 4.4 Backtracking
    5. 4.5 Searching an Array
  5. 5. Vector and Deques
    1. 5.1 Vector
    2. 5.2 High-Precision Arithmetic
    3. 5.3 Deques
  6. 6. Lists
  7. 7. Queue & Stacks
    1. 7.1 Queue
  8. 8.Binary & Search Tree
    1. 8.1 Binary Trees
    2. 8.2 External Path
    3. 8.3 Traversals of a binary tree
    4. 8.4 Binary Search Trees
  9. 9. AVL Tree
    1. 9.1 AVL Tree
    2. 9.2 The AVLTree Class
  10. 9. Red-Black Trees
    1. 9.1 Basically definition
    2. 9.2 Insertion Method
    3. 9.3 Erase Method